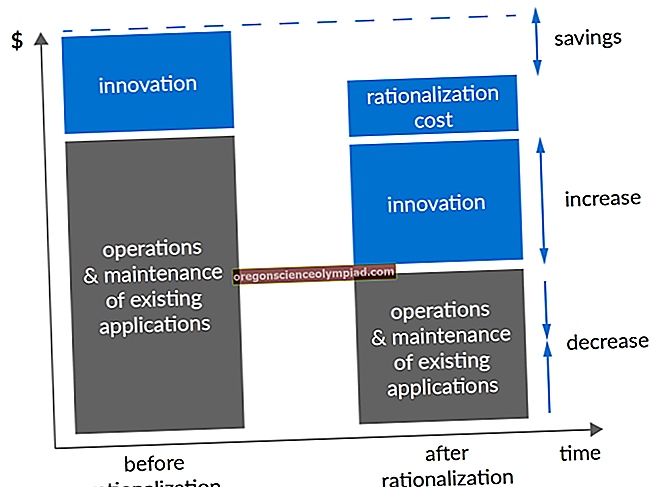
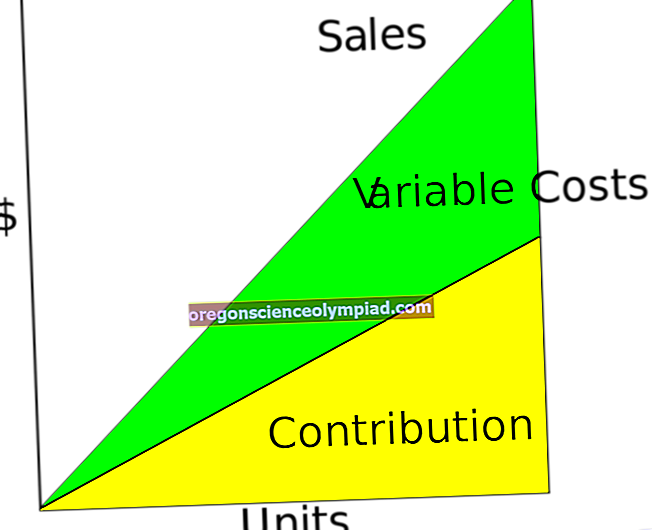
Diskontovaný peněžní tok je technika, která určuje současnou hodnotu budoucích peněžních toků. Podle této metody platí diskontní sazba pro každý pravidelný peněžní tok, který je odvozen z kapitálových nákladů účetní jednotky. Vynásobením této slevy každým budoucím peněžním tokem získáte částku, která je v souhrnu současnou hodnotou všech budoucích peněžních toků.
Výpočtem diskontovaných peněžních toků pro řadu různých investičních možností lze vybrat alternativu, která vede k největším diskontovaným peněžním tokům. Tento koncept je užitečný pro výpočet hodnoty potenciální akvizice, možné anuitní investice nebo nákupu dlouhodobého majetku.
Základem analýzy diskontovaných peněžních toků je koncept, že dnes přijatá hotovost je cennější než hotovost přijatá někdy v budoucnu. Důvodem je, že někdo, kdo souhlasí s přijetím platby později, se vzdává možnosti investovat tuto hotovost právě teď. Jediným způsobem, jak někdo souhlasit se zpožděnou výplatou, je zaplatit mu privilegium, které se označuje jako úrokový příjem.
Například pokud osoba nyní vlastní 10 000 $ a investuje ji s úrokovou sazbou 10%, vydělala 1 000 $ tím, že peníze použila po dobu jednoho roku. Pokud by místo toho neměla přístup k této hotovosti po dobu jednoho roku, ztratila by úrok z úroků ve výši 1 000 USD. Úrokový výnos v tomto příkladu představuje časovou hodnotu peněz.
Dvě analytické metody, které využívají koncept diskontovaných peněžních toků, jsou čistá současná hodnota a vnitřní míra návratnosti, které jsou popsány dále.
Čistá současná hodnota
Analýza čisté současné hodnoty (NPV) je užitečná pro stanovení aktuální hodnoty proudu peněžních toků, které sahají do budoucnosti. Lze jej také použít k porovnání několika takových peněžních toků k rozhodnutí, která má největší současnou hodnotu. NPV se běžně používá při analýze požadavků na nákup kapitálu, aby se zjistilo, zda počáteční platba za dlouhodobý majetek a další výdaje vygeneruje čisté kladné peněžní toky.
Pro výpočet čisté současné hodnoty použijeme následující vzorec:
NPV = X × [(1 + r) ^ n - 1] / [r × (1 + r) ^ n]
Kde:
X = částka přijatá za období
n = počet období
r = míra návratnosti
Vnitřní míra návratnosti
Interní míra návratnosti (IRR) je míra návratnosti, při které se současná hodnota řady budoucích peněžních toků rovná současné hodnotě všech souvisejících nákladů. IRR se běžně používá při kapitálovém rozpočtování k rozlišení míry návratnosti odhadovaných peněžních toků vyplývajících z očekávané investice. Pro investiční účely je vybrán projekt s nejvyšší IRR.
Nejjednodušší způsob, jak vypočítat interní míru návratnosti, je otevřít Microsoft Excel a potom postupujte takto:
- Do libovolné buňky zadejte záporné číslo, které představuje částku odtoku hotovosti v prvním období. To je normální, když pořizujete dlouhodobý majetek, protože na jeho pořízení a instalaci jsou počáteční výdaje.
- Zadejte následující peněžní toky pro každé období následující po počátečních výdajích do buněk bezprostředně pod buňkou, kde byl zadán údaj o počátečním odlivu peněz.
- Otevřete funkci IRR a zadejte rozsah buněk, do kterého jste právě zadali položky. Interní míra návratnosti se vypočítá automaticky. Může být užitečné použít funkci Zvětšit desetinnou čárku ke zvýšení počtu desetinných míst ve vypočítané vnitřní míře návratnosti.
Jako příklad společnost přezkoumává možnou investici, u níž je počáteční očekávaná investice ve výši 20 000 USD v prvním roce, následovaná příchozími peněžními toky ve výši 12 000 USD, 7 000 USD a 4 000 USD v příštích třech letech. Pokud tyto informace zadáte do funkce IRR aplikace Excel, vrátí IRR 8,965%.